Difference Between One-tailed and Two-tailed Test

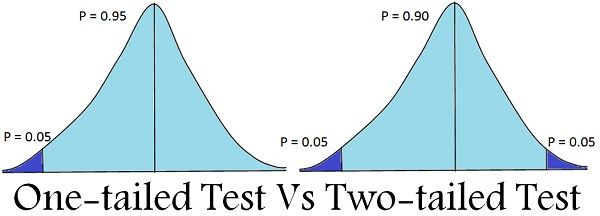
One tailed vs two tailed test

The two ways of carrying out statistical significance test of a characteristic, drawn from the population, with respect to the test statistic, are a one-tailed test and two-tailed test. The one-tailed test refers to a test of null hypothesis, in which the alternative hypothesis is articulated directionally. Here, the critical region lies only on one tail. However, if the alternative hypothesis is not exhibited directionally, then it is known as the two-tailed test of the null hypothesis., wherein the critical region is one both the tails.

To test the hypothesis, test statistics is required, which follows a known distribution. In a test, there are two divisions of probability density curve, i.e. region of acceptance and region of rejection. the region of rejection is called as a critical region.

In the field of research and experiments, it pays to know the difference between one-tailed and two-tailed test, as they are quite commonly used in the process.

Content: One-tailed Test Vs Two-tailed Test

Comparison Chart
Definition
Key Differences
Conclusion

Comparison Chart

Basis of Comparison	One-tailed Test	Two-tailed Test
Meaning	A statistical hypothesis test in which alternative hypothesis has only one end, is known as one tailed test.	A significance test in which alternative hypothesis has two ends, is called two-tailed test.
Hypothesis	Directional	Non-directional
Region of rejection	Either left or right	Both left and right
Determines	If there is a relationship between variables in single direction.	If there is a relationship between variables in either direction.
Result	Greater or less than certain value.	Greater or less than certain range of values.
Sign in alternative hypothesis	> or α , is placed in any one of the two tails. One-tailed test can be:

Left-tailed test: When the population parameter is believed to be lower than the assumed one, the hypothesis test carried out is the left-tailed test.
Right-tailed test: When the population parameter is supposed to be greater than the assumed one, the statistical test conducted is a right-tailed test.

Definition of Two-tailed Test

The two-tailed test is described as a hypothesis test, in which the region of rejection or say the critical area is on both the ends of the normal distribution. It determines whether the sample tested falls within or outside a certain range of values. Therefore, an alternative hypothesis is accepted in place of the null hypothesis, if the calculated value falls in either of the two tails of the probability distribution.

In this test, α is bifurcated into two equal parts, placing half on each side, i.e. it considers the possibility of both positive and negative effects. It is performed to see, whether the estimated parameter is either above or below the assumed parameter, so the extreme values, work as evidence against the null hypothesis.

Key Differences Between One-tailed and Two-tailed Test

The fundamental differences between one-tailed and two-tailed test, is explained below in points:

One-tailed test, as the name suggest is the statistical hypothesis test, in which the alternative hypothesis has a single end. On the other hand, two-tailed test implies the hypothesis test; wherein the alternative hypothesis has dual ends.
In the one-tailed test, the alternative hypothesis is represented directionally. Conversely, the two-tailed test is a non-directional hypothesis test.
In a one-tailed test, the region of rejection is either on the left or right of the sampling distribution. On the contrary, the region of rejection is on both the sides of the sampling distribution.
A one-tailed test is used to ascertain if there is any relationship between variables in a single direction, i.e. left or right. As against this, the two-tailed test is used to identify whether or not there is any relationship between variables in either direction.
In a one-tailed test, the test parameter calculated is more or less than the critical value. Unlike, two-tailed test, the result obtained is within or outside critical value.
When an alternative hypothesis has ‘≠’ sign, then a two-tailed test is performed. In contrast, when an alternative hypothesis has ‘> or

Conclusion

To sum up, we can say that the basic difference between one-tailed and two-tailed test lies in the direction, i.e. in case the research hypothesis entails the direction of interrelation or difference, then one-tailed test is applied, but if the research hypothesis does not signify the direction of interaction or difference, we use two-tailed test.

Comments

Swati Aggarwal says April 24, 2018 at 11:47 am

Very Informative and specifically summarised. thank you.

Amazing Surbhi. I recently started following this site and I really find it very very useful. The simplicity of language, the key distinctions, range of depth covered in giving the differences. Hats off to you for your effort. Very amazing. I have definitely bookmarked this website as ‘my favorite’ and I shall keep visiting it again and again. Keep it up. Thanks.